Grup poliedric

Deși acest articol conține o listă de referințe bibliografice, sursele sale rămân neclare deoarece îi lipsesc notele de subsol. Puteți ajuta introducând citări mai precise ale surselor. Întrucât este un articol tradus, a se vedea pagina de discuție, iar articolul de origine nu are nici el note de subsol, puteți ajuta și supraveghind acel articol, iar când acolo apar note de subsol, copiați-le și aici.

Grupuri punctuale în spațiul tridimensional

Simetrie involutivă Cs, (*) =	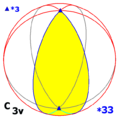Simetrie ciclică Cnv, (*nn) =	Simetrie diedrală Dnh, (*n22) =
Grup poliedric, , (*n32)
Simetrie tetraedrică Td, (*332) =	Simetrie octaedrică Oh, (*432) =	Simetrie icosaedrică Ih, (*532) =

În geometrie un grup poliedric este oricare din grupurile de simetrie ale poliedrelor platonice.

Există trei grupuri poliedrice:

• Grupul tetraedric de ordinul 12, grupul de simetrie rotațională al tetraedrului regulat. Este izomorf cu A₄.

• Clasele de conjugare^⁠(d) ale T sunt:

• identitatea
• 4 × rotație cu 120° în sens trigonometric, ordin 3
• 4 × rotație cu 120° în sens orar, ordin 3
• 3 × rotație cu 180°, ordin 2

• Grupul octaedric de ordinul 24, grupul de simetrie rotațională al cubului și octaedrului regulat. Este izomorf cu S₄.

• Clasele de conjugare ale O sunt:

• identitatea
• 6 × rotație cu ±90° în jurul vârfurilor, ordin 4
• 8 × rotație cu ±120° în jurul centrelor triunghiurilor, ordin 3
• 3 × rotație cu 180° în jurul vârfurilor, ordin 2
• 6 × rotație cu 180° în jurul mijloacelor laturilor, ordin 2

• Grupul icosaedric de ordinul 60, grupul de simetrie rotațională al dodecaedrului regulat și al icosaedrului regulat. Este izomorf cu A₅.

• Clasele de conjugare ale I sunt:

• identitatea
• 12 × rotație cu ±72°, ordin 5
• 12 × rotație cu ±144°, ordin 5
• 20 × rotație cu ±120°, ordin 3
• 15 × rotație cu 180°, ordin 2

Aceste simetrii se dublează la 24, 48, respectiv 120 pentru grupurile de reflexie complete. Simetriile de reflexie au 6, 9 și respectiv 15 plane de oglindire. Simetria octaedrică, poate fi văzută ca reunirea a 6 plane de oglindire de simetrie tetraedrică și a 3 plane de oglindire de simetrie diedrală Dih₂, . Simetria piritoedrică este o altă dublare a simetriei tetraedrice.

Clasele de conjugare ale simetriei tetraedrice complete, T_d≅S₄, sunt:

• identitatea
• 8 × rotație cu 120°
• 3 × rotație cu 180°
• 6 × reflexie în plan față de două axe
• 6 × rotație improprie cu 90°

Clasele de conjugare ale simetriei piritoedrice, T_h, le cuprind pe cele ale lui T, cu cele două clase de 4 combinate și fiecare cu inversare:

• identitatea
• 8 × rotație cu 120°
• 3 × rotație cu 180°
• inversiunea
• 8 × rotație improprie cu 60°
• 3 × reflexie în plan

Clasele de conjugare ale grupului octaedric complet, O_h≅S₄ × C₂, sunt:

• inversiunea
• 6 × rotație improprie cu 90°
• 8 × rotație improprie cu 60°
• 3 × reflexie în plan perpendicular pe o axă, cu 4 poziții
• 6 × reflexie în plan perpendicular pe o axă, cu 2 poziții

Clasele de conjugare ale grupului icosaedric complet, I_h≅A₅ × C₂, sunt:

• inversiunea
• 12 × rotație improprie cu 108°, ordin 10
• 12 × rotație improprie cu 36°, ordin 10
• 20 × rotație improprie cu 60°, ordin 6
• 15 × reflexie, ordin 2

Grupuri poliedrice chirale

Nume (Orb.)	Notația Coxeter	Ordin	Structură abstractă	Puncte de rotație #valență	Diagrame
					Ortogonal	Stereografic
T (332)	+	12	A4	43 32
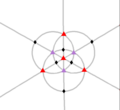
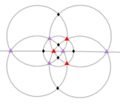
Th (3*2)		24	A4×2	43 3*2
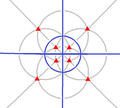
O (432)	+	24	S4	34 43 62
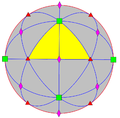
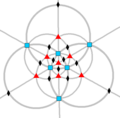
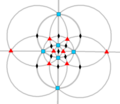
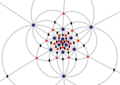
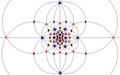
I (532)	+	60	A5	65 103 152

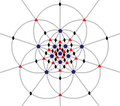
Grupuri poliedrice complete

Weyl Schoe. (Orb.)	Notația Coxeter	Ordin	Structură abstractă	Număr Coxeter (h)	Oglinzi (m)	Diagrame ale oglindirilor
						Ortogonal	Stereografic
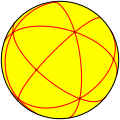
A3 Td (*332)		24	S4	4	6
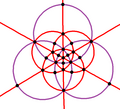
B3 Oh (*432)		48	S4×2	8	3 6
H3 Ih (*532)		120	A5×2	10	15

• Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, 1973. (The Polyhedral Groups. §3.5, pp. 46–47)

Portal Matematică

• en Eric W. Weisstein, PolyhedralGroup la MathWorld.