Simetrie de reflexie

În lumea de astăzi, Simetrie de reflexie este un subiect de mare relevanță și dezbatere. Odată cu progresul tehnologiei și globalizarea, Simetrie de reflexie a devenit un element cheie în societatea noastră, având impact asupra diferitelor aspecte ale vieții de zi cu zi. De la economie la politică, Simetrie de reflexie a generat discuții și reflecții în toate domeniile. De aceea, este esențial să analizăm temeinic acest fenomen, să înțelegem implicațiile lui și să căutăm soluții la provocările pe care le prezintă. În acest articol, vom explora diferite perspective asupra Simetrie de reflexie, de la originea sa până la impactul său astăzi, cu scopul de a oferi o imagine de ansamblu completă și îmbogățitoare a acestui subiect foarte relevant.

Figuri cu axele de simetrie desenate. Figura fără axe este asimetrică

În matematică simetria de reflexie, simetrie axială[1], simetria față de o dreaptă sau simetria în oglindă este simetria cu privire la o reflexie. Adică, o figură care nu se schimbă în urma unei reflexii are simetrie de reflexie.

Într-un spațiu bidimensional simetria este față de o dreaptă (axă de simetrie), iar într-un spațiu tridimensional față de un plan de simetrie. Un obiect sau o figură a cărei imagine nu se poate distinge de imaginea sa reflectată sunt simetrice în oglindă. În fapt, o dreaptă, respectiv un plan de simetrie împarte forma în două jumătăți care ar trebui să fie identice.

Funcție simetrică

O curbă „clopot” de distribuție normală este un exemplu de funcție simetrică

În termeni formali, un obiect matematic este simetric în raport cu o operație dată, cum ar fi reflexia, rotația sau translația, dacă, atunci când este aplicată obiectului, această operație conservă unele proprietăți ale obiectului.[2] Setul de operații care conservă o proprietate dată a obiectului formează un grup. Două obiecte sunt simetrice unul față de celălalt în raport cu un grup dat de operații dacă unul este obținut din celălalt prin unele operații (și invers).

Funcția de simetrie a unei figuri bidimensionale este o dreaptă astfel încât, pentru orice perpendiculară construită pe ea, dacă perpendiculara intersectează figura la o distanță d de axa de-a lungul perpendicularei, atunci există o altă intersecție a formei cu perpendiculara, la aceeași distanță d de axă, dar în sens invers de-a lungul perpendicularei.

Un alt mod de a ne reprezenta funcția simetrică este acela prin care dacă forma ar fi pliată în jumătate de-a lungul axei, cele două jumătăți ar fi identice: fiecare din cele două jumătăți este imaginea în oglindă a celeilalte.[2]

Astfel, un pătrat are patru axe de simetrie, deoarece există patru moduri diferite de a-l plia astfel încât toate laturile sale să se suprapună. Un cerc are un număr infinit de axe de simetrie.

Forme geometrice simetrice

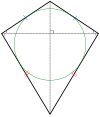
Forme bidimensionale cu simetrie de reflexie
trapez isoscel și romboid
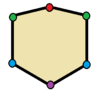
hexagoane
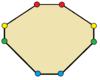
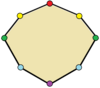
octogoane

Triunghiurile cu simetrie de reflexie sunt isoscele. Patrulaterele cu simetrie de reflexie sunt romburile, romboizii (inclusiv concavi),[3] și trapezele isoscele. Toate poligoanele regulate au două forme de reflexie simple, una cu axe de simetrie prin vârfuri și una cu axe prin mijlocul laturilor.

Pentru o formă arbitrară, axialitatea formei măsoară cât de aproape este de a fi simetrică bilateral. Este egală cu 1 pentru formele cu simetrie de reflexie și între 2/3 și 1 pentru orice formă convexă.

Forme avansate de simetrie de reflexie

Pentru tipuri mai generale de reflexii există, corespunzător, mai multe tipuri generale de simetrie de reflexie. De exemplu:

  • cu privire la o involuție afină neizometrică (o reflexie oblică față de o dreaptă, un plan etc.)
  • cu privire la inversiunea cercului⁠(d).

În natură

Multe animale, cum ar fi acest crab Maja crispata, au simetrie bilaterală

Animalele care sunt simetrice bilateral au simetrie de reflexie în planul sagital, care împarte corpul pe verticală în jumătăți stângă și dreaptă, cu câte unul din fiecare organ de simț și pereche de membre de fiecare parte. Majoritatea animalelor sunt simetrice bilateral, probabil pentru că acest lucru favorizează mișcarea înainte în linie dreaptă.[4][5][6][7]

În arhitectură

Simetria în oglindă este adesea folosită în arhitectură, ca la fațada bisericii Santa Maria Novella din Florența, 1470

Simetria în oglindă este adesea folosită în arhitectură, ca la fațada bisericii Santa Maria Novella din Florența.[8] Se găsește și în structurile antice, cum ar fi Stonehenge.[9] Simetria a fost un element de bază în unele stiluri de arhitectură, cum ar fi palladianismul.[10]

Note

  1. ^ Oana Constantinescu, Grupuri de simetrii (curs), Universitatea „Alexandru Ioan Cuza” din Iași, accesat 2024-05-18
  2. ^ a b en Stewart, Ian (). What Shape is a Snowflake? Magical Numbers in Nature. Weidenfeld & Nicolson. p. 32. 
  3. ^ en Gullberg, Jan (). Mathematics: From the Birth of NumbersNecesită înregistrare gratuită. W. W. Norton. pp. 394–395. ISBN 0-393-04002-X. 
  4. ^ en Valentine, James W. „Bilateria”. AccessScience. Accesat în . 
  5. ^ en „Bilateral symmetry”. Natural History Museum. Accesat în . 
  6. ^ en Finnerty, John R. (). „Did internal transport, rather than directed locomotion, favor the evolution of bilateral symmetry in animals?” (PDF). BioEssays. 27 (11): 1174–1180. doi:10.1002/bies.20299. PMID 16237677. Arhivat din original (PDF) la . Accesat în . 
  7. ^ en „Bilateral (left/right) symmetry”. Berkeley. Accesat în . 
  8. ^ en Tavernor, Robert (). On Alberti and the Art of Building. Yale University Press. pp. 102–106. ISBN 978-0-300-07615-8. More accurate surveys indicate that the facade lacks a precise symmetry, but there can be little doubt that Alberti intended the composition of number and geometry to be regarded as perfect. The facade fits within a square of 60 Florentine braccia 
  9. ^ en Johnson, Anthony (2008). Solving Stonehenge: The New Key to an Ancient Enigma. Thames & Hudson.
  10. ^ en Waters, Suzanne. „Palladianism”. Royal Institution of British Architects. Arhivat din original la . Accesat în . 

Bibliografie

  • en Stewart, Ian (). What Shape is a Snowflake? Magical Numbers in Nature. Weidenfeld & Nicolson. 
  • en Weyl, Hermann () . Symmetry. Princeton: Princeton University Press. ISBN 0-691-02374-3. 

Vezi și

Legături externe

Materiale media legate de simetrie de reflexie la Wikimedia Commons

Portal icon Portal Matematică