Micul dodecaedru trunchiat stelat

Micul dodecaedru trunchiat stelat
(model 3D)
Descriere
Tip	poliedru uniform neconvex
Fețe	24 (12 pentagoane,       12 decagrame)
Laturi (muchii)	90
Vârfuri	60
χ	−6
Configurația vârfului	5.10/3.10/3[1]
Simbol Wythoff	2 5 | 5/3[1] sau 2 5/4 | 5/3
Simbol Schläfli	t{5/3,5}
Diagramă Coxeter
Grup de simetrie	Ih, , (*532) [1]
Volum	≈4,698 a3   (a = latura)
Poliedru dual	marele dodecaedru pentakis
Proprietăți	uniform, neconvex
Figura vârfului

În geometrie micul dodecaedru trunchiat stelat este un poliedru stelat uniform, cu indicele U₅₈. Are 24 de fețe (12 pentagoane și 12 decagrame), 90 de laturi și 60 de vârfuri.^[1] Având 24 de fețe este un icositetraedru neconvex. Un poliedru neconvex are fețe care se intersectează care nu reprezintă laturi sau fețe noi. Doar cele marcate cu sfere aurii sunt vârfuri, iar cele cu linii argintii sunt laturi.

Are simbolul Wythoff 2 5 | 5/3,^[1][2] simbolul Schläfli t{5/3,5}, și diagrama Coxeter .

Având în comun vârfurile cu compusul de șase prisme pentagramice, coordonatele carteziene ale vârfurilor sale cu lungimea laturii 2, centrat în origine, sunt toate permutările ale^[3][4]

${\displaystyle \left(\,\pm \varphi ,\,\pm (2-\varphi ),\,\pm (2-\varphi )\,\right)}$

plus toate permutările pare ale

${\displaystyle \left(\,0,\,\pm 1,\,\pm (3-\varphi )\,\right)}$

${\displaystyle \left(\,\pm 1,\,\pm (\varphi -1),\,\pm (\varphi -1)\,\right)}$

unde ${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}$ este secțiunea de aur.

Raza circumscrisă în funcție de lungimea laturilor a este:^[5]

${\displaystyle R={\frac {1}{4}}{\sqrt {34-10{\sqrt {5}}}}\,a\approx 0,852911\,a.}$

Următoarea formulă pentru volum V este stabilită pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a este:

${\displaystyle V={\frac {11}{4}}\left(3{\sqrt {5}}-5\right)\,a^{3}\approx 4,697561~a^{3}.}$

Acest compus are în comun aranjamentul vârfurilor cu trei poliedre uniforme: rombicosidodecaedrul, micul dodecicosidodecaedru și micul rombidodecaedru și cu doi compuși poliedrici uniformi: compusul de șase prisme pentagramice și compusul de douăsprezece prisme pentagramice.

Rombicosidodecaedru	Micul dodecicosidodecaedru	Micul rombidodecaedru
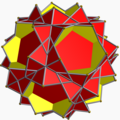Micul dodecaedru stelat trunchiat	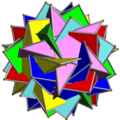Compus de șase prisme pentagramice	Compus de douăsprezece prisme pentagramice

Dualul său este marele dodecaedru pentakis.^[6]

• Lista poliedrelor uniforme

• en Uniform polyhedra and duals

Portal Matematică

• en Klitzing, Richard. „3D uniform polyhedra”.  Cheie: quit sissid