Micul dodecicosidodecaedru

Micul dodecicosidodecaedru
(model 3D)
Descriere
Tip	poliedru uniform neconvex
Fețe	44 (20 triunghiuri       12 pentagoane       12 decagoane)
Laturi (muchii)	120
Vârfuri	60
χ	−16
Configurația vârfului	5.10.3/2.10[1]
Simbol Wythoff	3/2 5 | 5[1] sau 3 5/4 | 5
Diagramă Coxeter
Grup de simetrie	Ih, , (*532) [1]
Volum	≈55,342 a3   (a = latura)
Poliedru dual	micul hexaconatedru dodecacronic
Proprietăți	uniform, neconvex
Figura vârfului

În geometrie micul dodecicosidodecaedru este un poliedru uniform neconvex, cu indicele U₃₃. Are 44 de fețe (20 de pătrate, 12 pentagoane și 12 decagoane), 120 de laturi și 60 de vârfuri.^[1][2] Având 44 de fețe, este un tetracontatetraedru.

Este reprezentat prin diagramele Coxeter–Dynkin . Figura vârfului este un patrulater autointersectat. Un poliedru neconvex are fețe care se intersectează care nu reprezintă laturi sau fețe noi. Doar cele marcate cu sfere aurii sunt vârfuri, iar cele cu linii argintii sunt laturi.

Are simbolul Wythoff 3/2 5 | 5^[1] sau 3 5/4 | 5.

Coordonatele carteziene ale vârfurilor unui mic dodecicosidodecaedru centrat în origine, cu lungimea laturii de 2, sunt toate permutările pare ale:^[3][4]

${\displaystyle \left(\,\pm (1+2\varphi ),\,\pm 1,\,\pm 1\,\right)}$

${\displaystyle \left(\,0,\,\pm (1+\varphi ),\,\pm (2+\varphi )\,\right)}$

${\displaystyle \left(\,\pm \varphi ,\,\pm \varphi ,\,\pm (1+\varphi )\,\right)}$

unde ${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}$ este secțiunea de aur.

Raza sferei circumscrise este distanța comună a vârfurilor față de origine, și anume ${\displaystyle {\sqrt {\varphi ^{6}+2}}={\sqrt {8\varphi +7}}}$ pentru lungimea laturii egală cu 2. Pentru lungimea laturii a, această valoare devine:^[2]

${\displaystyle R={\frac {\sqrt {8\varphi +7}}{2}}\,a={\frac {\sqrt {11+4{\sqrt {5}}}}{2}}\,a\approx 2,232951\,a.}$

Următoarea formulă pentru volum V este stabilită pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:

${\displaystyle V=\left(30+{\frac {34}{3}}{\sqrt {5}}\right)\,a^{3}\approx 55,342104\,a^{3}}$

Are în comun aranjamentul vârfurilor cu micul dodecaedru trunchiat stelat, compusul de șase prisme pentagramice și compusul de douăsprezece prisme pentagramice. În plus, are în comun aranjamentul laturilor cu rombicosidodecaedrul (având fețele triunghiulare în comun) și cu micul rombidodecaedru (având fețele decagonale în comun).

Rombicosidodecaedru	Micul dodecicosidodecaedru	Micul rombidodecaedru
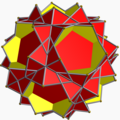Micul dodecaedru trunchiat stelat	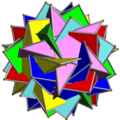Compus de șase prisme pentagramice	Compus de douăsprezece prisme pentagramice

Dualul său este micul hexaconatedru dodecacronic.^[5]

• en Coxeter, H. S. M. (13 mai 1954). „Uniform Polyhedra”. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences. 246 (916): 401–450. doi:10.1098/rsta.1954.0003. 
• en Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9. OCLC 1738087. 

• Lista poliedrelor uniforme

• en Uniform polyhedra and duals

Portal Matematică

• en Klitzing, Richard. „3D uniform polyhedra”.  Cheie: saddid