Pavare apeirogonală de ordin infinit

În lumea de astăzi, Pavare apeirogonală de ordin infinit a devenit din ce în ce mai important în diferite aspecte ale vieții de zi cu zi. Fie la nivel personal, profesional sau social, Pavare apeirogonală de ordin infinit a devenit un element fundamental care ne influențează deciziile, opiniile și acțiunile. De-a lungul timpului, Pavare apeirogonală de ordin infinit a evoluat și a dobândit noi dimensiuni, determinându-ne să reflectăm asupra impactului său asupra societății și asupra dezvoltării umanității. În acest articol, vom explora diferitele fațete ale Pavare apeirogonală de ordin infinit și vom analiza relevanța acestuia în diverse contexte, precum și rolul său în modelarea lumii noastre de astăzi.

Deși acest articol conține o listă de referințe bibliografice, sursele sale rămân neclare deoarece îi lipsesc notele de subsol.
Puteți ajuta introducând citări mai precise ale surselor.
Întrucât este un articol tradus, a se vedea pagina de discuție, iar articolul de origine nu are nici el note de subsol, puteți ajuta și supraveghind acel articol, iar când acolo apar note de subsol, copiați-le și aici.
Pavare apeirogonala
de ordin infinit
Pe modelul discului Poincaré al planului hiperbolic
Descriere
Tippavare uniformă hiperbolică
Configurația vârfului∞∞
Simbol Wythoff∞ | ∞ 2
∞ ∞ | ∞
Simbol Schläfli{∞,∞}
Diagramă Coxeter
Grup de simetrie, (*∞∞2)
, (*∞∞∞)
Grup de rotație+, (∞∞2)
+, (∞∞∞)
Poliedru dualautoduală
Proprietățitranzitivă pe vârfuri, laturi și fețe

În geometrie pavarea apeirogonală de ordin infinit este o pavare regulată a planului hiperbolic. Este reprezentată de simbolul Schläfli {∞,∞}, având un număr (numărabil) infinit de apeirogoane în jurul fiecărui vârf. Toate vârfurile sunt ideale, situate la „infinit” și văzute la limita proiecției pe discul hiperbolic Poincaré.

Simetrie

Această pavare reprezintă domeniile fundamentale ale simetriei *∞∞.

Colorare uniformă

Această pavare poate fi colorată alternativ în simetria din 3 poziții ale generatorului.

Domenii 0 1 2

simetrie:
 
t0{(∞,∞,∞)}
t1{(∞,∞,∞)}
t2{(∞,∞,∞)}

Poliedre și pavări înrudite

Pavarea duală
{∞,∞} sau = ∪
Pavarea apeirogonală de ordin infinit împreună cu duala sa

Reuniunea acestei pavări cu duala sa poate fi văzută aici ca linii roșii și albastre ortogonale, iar combinate definesc liniile unui domeniu fundamental *2∞2∞.

Pavări uniforme paracompacte din familia

=
=
=
=
=
=
=
=
=
=
=
=
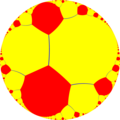
{∞,∞} t{∞,∞} r{∞,∞} 2t{∞,∞}=t{∞,∞} 2r{∞,∞}={∞,∞} rr{∞,∞} tr{∞,∞}
Pavări duale
V∞∞ V∞.∞.∞ V(∞.∞)2 V∞.∞.∞ V∞∞ V4.∞.4.∞ V4.4.∞
Alternări

(*∞∞2)
(∞*∞)
(*∞∞∞∞)
(∞*∞)
(*∞∞2)
(2*∞∞) 		+
(2∞∞)
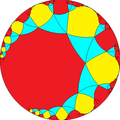
h{∞,∞} s{∞,∞} hr{∞,∞} s{∞,∞} h2{∞,∞} hrr{∞,∞} sr{∞,∞}
Duale alternate
V(∞.∞)∞ V(3.∞)3 V(∞.4)4 V(3.∞)3 V∞∞ V(4.∞.4)2 V3.3.∞.3.∞
Pavări uniforme paracompacte din familia
(∞,∞,∞)
h{∞,∞} 		r(∞,∞,∞)
h2{∞,∞} 		(∞,∞,∞)
h{∞,∞} 		r(∞,∞,∞)
h2{∞,∞} 		(∞,∞,∞)
h{∞,∞} 		r(∞,∞,∞)
r{∞,∞} 		t(∞,∞,∞)
t{∞,∞}
Pavări duale
V∞∞ V∞.∞.∞.∞ V∞∞ V∞.∞.∞.∞ V∞∞ V∞.∞.∞.∞ V∞.∞.∞
Alternări

(*∞∞∞∞)
(∞*∞)
(*∞∞∞∞)
(∞*∞)
(*∞∞∞∞)
(∞*∞) 		+
(∞∞∞)
Duale alternate
V(∞.∞)∞ V(∞.4)4 V(∞.∞)∞ V(∞.4)4 V(∞.∞)∞ V(∞.4)4 V3.∞.3.∞.3.∞

Bibliografie

  • en John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN: 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
  • en „Chapter 10: Regular honeycombs in hyperbolic space”. The Beauty of Geometry: Twelve Essays. Dover Publications. . ISBN 0-486-40919-8. LCCN 99035678. 

Vezi și

Legături externe

Portal icon Portal Matematică