Poliedru sferic

Astăzi, subiectul Poliedru sferic este de maximă importanță și a captat atenția a milioane de oameni din întreaga lume. Fie datorită impactului său asupra societății, a relevanței sale astăzi, fie pur și simplu datorită istoriei sale fascinante, Poliedru sferic a reușit să devină un subiect de dezbatere constantă. De la începuturile sale și până la posibilele sale repercusiuni în viitor, Poliedru sferic s-a dovedit a fi un subiect interesant care merită să fie explorat în profunzime. Pe parcursul acestui articol, vom aprofunda diferitele aspecte ale Poliedru sferic, analizând originile, evoluția și posibilele scenarii viitoare.

Cel mai cunoscut poliedru sferic este mingea de fotbal, gândită ca un icosaedru trunchiat sferic
Această minge de plajă ar fi un hosoedru cu 6 fețe în formă de fusuri sferice dacă cele 2 petice albe de la poli ar fi îndepărtate

În matematică un poliedru sferic sau pavare sferică este o teselare a sferei în care suprafața ei este împărțită de arce de cercuri mari în regiuni mărginite numite poligoane sferice. O mare parte din teoria poliedrelor simetrice este prezentată mai convenabil în acest mod.

Cel mai cunoscut poliedru sferic este mingea de fotbal, gândită ca un icosaedru trunchiat sferic Următorul poliedru sferic cel mai popular este mingea de plajă, considerată drept hosoedru.

Unele cazuri „improprii” de poliedre, cum ar fi hosoedrele și dualele lor, diedrele, există ca poliedre sferice, dar analoagele lor cu fețe plane sunt degenerate. Exemplul de minge de plajă hexagonală, {2, 6}, este un hosoedru, iar {6, 2} este diedrul său dual.

Istoric

Primele poliedre artificiale cunoscute sunt poliedrele sferice cioplire în piatră. Multe au fost găsite în Scoția și par să dateze din neolitic.

În secolul al X-lea savantul islamic Abū al-Wafā' Būzjānī (Abu'l Wafa) a scris primul studiu serios despre poliedrele sferice.

Acum două sute de ani, la începutul secolului al XIX-lea, Poinsot a folosit poliedre sferice pentru a descoperi cele patru poliedre stelate regulate.

La mijlocul secolului al XX-lea, Coxeter le-a folosit pentru a enumera toate poliedrele uniforme, cu excepția unuia, prin realizarea de caleidoscoape (construcția Wythoff).

Exemple

Toate poliedrele regulate, semiregulate și dualele lor pot fi proiectate pe sferă sub formă de pavări:

Simbol
Schläfli 		{p,q} t{p,q} r{p,q} t{q,p} {q,p} rr{p,q} tr{p,q} sr{p,q}
Configurația
vârfului 		pq q.2p.2p p.q.p.q p.2q.2q qp q.4.p.4 4.2q.2p 3.3.q.3.p
Simetrie
tetraedrică
(3 3 2)
33
3.6.6
3.3.3.3
3.6.6
33
3.4.3.4
4.6.6
3.3.3.3.3

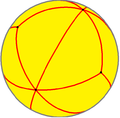V3.6.6
V3.3.3.3
V3.6.6
V3.4.3.4
V4.6.6
V3.3.3.3.3
Simetrie
octaedrică
(4 3 2)
43
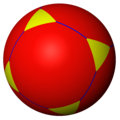3.8.8
3.4.3.4
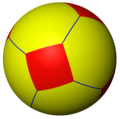4.6.6
34
3.4.4.4
4.6.8
3.3.3.3.4

V3.8.8
V3.4.3.4
V4.6.6
V3.4.4.4
V4.6.8
V3.3.3.3.4
Simetrie
icosaedrică
(5 3 2)
53
3.10.10
3.5.3.5
5.6.6
35
3.4.5.4
4.6.10
3.3.3.3.5

V3.10.10
V3.5.3.5
V5.6.6
V3.4.5.4
V4.6.10
V3.3.3.3.5
Exemplu
diedral p=6
(2 2 6)
62
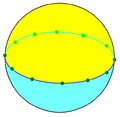2.12.12
2.6.2.6
6.4.4
26
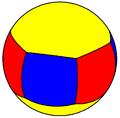2.4.6.4
4.4.12
3.3.3.6
Pavarea sferei cu triunghiuri sferice (icosaedru cu unele dintre triunghiurile sale sferice distorsionate)
n 2 3 4 5 6 7 8 10 ...
n-prismă
(2 2 p) 		...
n-bipiramidă
(2 2 p) 		...
n-antiprismă ...
n-trapezoedru ...

Cazuri improprii

Pavările sferice permit cazuri care nu par poliedre, și anume, hosoedre (figuri ca {2,n}) și diedre (figuri ca {n,2}). În general, se folosesc hosoedre și diedre regulate.

Familia hosoedrelor regulate cu simetrie *n22 , repectiv pavări hosoedrice regulate nn
Spațiu Sferic Euclidian
Denumirea pavării (Monogonală)
hosoedru henagonal
hosoedru digonal 		(Triunghiulară)
hosoedru trigonal 		(Pătrată)
hosoedru tetragonal
hosoedru pentagonal
hosoedru hexagonal
...
hosoedru apeirogonal
Imagine ...
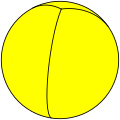
Simbol Schläfli {2,1} {2,2} {2,3} {2,4} {2,5} {2,6} ... {2,∞}
Diagramă Coxeter ...
Fețe și laturi 1 2 3 4 5 6 ... ∞
Vârfuri 2 ... 2
Config. vârf 2 2.2 23 24 25 26 ... 2∞
Familia diedrelor regulate: *n22 permutări simetrice ale pavărilor diedrice regulate nn
Spațiu Sferic Euclidian
Denumirea pavării (Hengonală)
Diedru monogonal 		(Digonală)
Diedru digonal 		(Triunghiulară)
Diedru triunghiular 		(Pătratică)
Diedru pătrat 		Diedru pentagonal Diedru hexagonal ... Diedru apeirogonal
Imaginea pavării ...
Simbol Schläfli {1,2} {2,2} {3,2} {4,2} {5,2} {6,2} ... {∞,2}
Diagramă Coxeter ...
Fețe 2 {1} 2 {2} 2 {3} 2 {4} 2 {5} 2 {6} ... 2 {∞}
Laturi și vârfuri 1 2 3 4 5 6 ... ∞
Config. vârf 1.1 2.2 3.3 4.4 5.5 6.6 ... ∞.∞

Relația cu pavările planului proiectiv

Poliedre sferice care au cel puțin o simetrie inversă sunt legate de poliedrele proiective⁠(d)[1] (teselări ale planului proiectiv real⁠(d)) — așa cum sfera are o acoperire de 2 la 1 a planului proiectiv, poliedrele proiective corespund cu o acoperire dublă poliedrelor sferice care sunt simetrice față de centru.

Cele mai cunoscute exemple de poliedre proiective sunt poliedre proiective regulate, corespondentele poliedrelor platonice cu simetrie centrală, precum și două clase infinite de diedre și hosoedre:[2]

Note

  1. ^ en McMullen, Peter; Schulte, Egon (). „6C. Projective Regular Polytopes”. Abstract Regular Polytopes. Cambridge University Press. pp. 162–5. ISBN 0-521-81496-0. 
  2. ^ en Coxeter, H.S.M. (). „§21.3 Regular maps'”. Introduction to GeometryAcces gratuit pentru testarea serviciului, necesită altfel abonament (ed. 2nd). Wiley. pp. 386–8. ISBN 978-0-471-50458-0. MR 0123930. 

Bibliografie

  • en Poinsot, L. (). „Memoire sur les polygones et polyèdres”. J. De l'École Polytechnique. 9: 16–48. 
  • en Coxeter, H.S.M.; Longuet-Higgins, M.S.; Miller, J.C.P. (). „Uniform polyhedra”. Phil. Trans. 246 A (916): 401–50. JSTOR 91532. 
  • en Coxeter, H.S.M. (). Regular Polytopes (ed. 3rd). Dover. ISBN 0-486-61480-8. 

Legături externe

Portal icon Portal Matematică