Hosoedru

Hosoedre regulate n-gonale
Exemplu de hosoedru hexagonal regulat pe o sferă
Tip	Poligon regulat sau pavare sferică
Laturi și vârfuri	n
Simbol Schläfli	{2,n}
Diagramă Coxeter
Grup de simetrie	Dnh, , (*22n), ordin 4n
Grup de rotație	Dn, +, (22n), ordin 2n
Poligon dual	diedru n-gonal regulat

În geometria sferică, un hosoedru n-gonal este o pavare de fusuri pe o suprafață sferică, astfel încât toate fusurile au în comun aceleași două vârfuri, situate la antipozi.

Un hosoedru n-gonal regulat are simbolul Schläfli {2, n}, fiecare fus sferic având unghiurile interne 2π/n radiani (360/n grade).^[1][2]

Termenul de „hosoedru” pare să provină din grecescul ὅσος (hosos = câte), ideea fiind că un hosoedru poate avea atâtea fețe cât se dorește.^[3] A fost introdus în secolul al XVIII-lea de Vito Caravelli.^[4]

Pentru un poliedru regulat al cărui simbol Schläfli este {m, n}, numărul de fețe poligonale este:

${\displaystyle N_{2}={\frac {4n}{2m+2n-mn}}.}$

Poliedrele platonice, cunoscute din antichitate, sunt singurele soluții întregi pentru m ≥ 3 și n ≥ 3. Restricția m ≥ 3 impune ca fețele poligonale să aibă la cel puțin trei laturi.

Când se consideră suprafața poliedrelor ca o pavare sferică această restricție poate fi relaxată, deoarece digoanele (2-goane) pot fi reprezentate ca fusuri sferice, având aria diferită de zero.

Cu m = 2 se obține

${\displaystyle N_{2}={\frac {4n}{2\times 2+2n-2n}}=n,}$

care formează o nouă clasă infinită de poliedre regulate, hosoedrele. Pe o suprafață sferică, poliedrul {2, n} este reprezentat ca n fusuri adiacente, cu unghiuri interioare de 2π/n. Toate aceste fusuri sferice au cele două vârfuri comune.

Un hosoedru trigonal regulat, {2,3}, reprezentat ca o teselare de 3 fusuri sferice pe o sferă

Un hosoedru tetragonal regulat, {2,4}, reprezentat ca o teselare de 4 fusuri sferice pe o sferă

Familia hosoedrelor regulate cu simetrie *n22 , repectiv pavări hosoedrice regulate nn

Spațiu	Sferic							Euclidian
Denumirea pavării	(Monogonală) hosoedru henagonal	hosoedru digonal	(Triunghiulară) hosoedru trigonal	(Pătrată) hosoedru tetragonal	hosoedru pentagonal	hosoedru hexagonal	...	hosoedru apeirogonal
Imagine							...
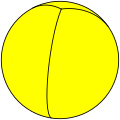
Simbol Schläfli	{2,1}	{2,2}	{2,3}	{2,4}	{2,5}	{2,6}	...	{2,∞}
Diagramă Coxeter							...
Fețe și laturi	1	2	3	4	5	6	...	∞
Vârfuri	2						...	2
Config. vârf	2	2.2	23	24	25	26	...	2∞

Cele 2n fețe în formă de fusuri sferice ale unui 2n-hosoedru, {2,2n}, reprezintă domeniile fundamentale ale simetriei diedrale tridimensionale: simetria cercului C_nv, , (*nn), ordin 2n. Domeniile de reflexie pot fi afișate prin fusuri colorate alternativ ca imagini în oglindă.

Divizarea fiecărui fus în două triunghiuri sferice creează o bipiramidă n-gonală, care reprezintă simetria diedrală D_nh, ordin 4n.

Simetrie (ordin 2n)	Cnv,	C1v,	C2v,	C3v,	C4v,	C5v,	C6v,
Hosoedru 2n-gonal	Simbol Schläfli {2,2n}	{2,2}	{2,4}	{2,6}	{2,8}	{2,10}	{2,12}
Imagine	Colorare alternată a domeniilor fundamentale

Poliedrul dual al hosoedrului n-gonal {2, n} este diedrul n-gonal, {n,  2}. Poliedrul {2,2} este autodual și este atât un hosoedru cât și un diedru.

Un hosoedru poate fi modificat în același mod ca și celelalte poliedre pentru a produce o variantă trunchiată. Hosoedrul n-gonal trunchiat este prisma n-gonală.

La limită, hosoedrul devine un hosoedru apeirogonal ca o teselare bidimensională:

Analoagele multidimensionale se numesc hosotopuri. Un hosotop regulat cu simbolul Schläfli {2,p,...,q} are două vârfuri, fiecare cu figura vârfului {p,. ..,q}.

Hosotopul bidimensional, {2}, este digonul.

• en Coxeter, H.S.M, Regular Polytopes (third edition), Dover Publications Inc., ISBN: 0-486-61480-8
• en McMullen, Peter; Schulte, Egon (decembrie 2002), Abstract Regular Polytopes (ed. 1st), Cambridge University Press, ISBN 0-521-81496-0 

Portal Matematică

• en Eric W. Weisstein, Hosohedron la MathWorld.