Antiprismă pentagonală

Descriere
Antiprismă pentagonală

(model 3D)
Tip	poliedru uniform, ca poliedru semiregulat
Fețe	12 (10 triunghiuri, 2 pentagoane)
Laturi (muchii)	20
Vârfuri	10
χ	2
Configurația vârfului	3.3.3.5
Simbol Wythoff	\| 2 2 5
Simbol Schläfli	s{2,10} sr{2,5}
Simbol Conway	A6
Diagramă Coxeter
Grup de simetrie	D_5d, , (2*6), ordin 20
Arie	≈ 7,771 a² (a = latura)
Volum	≈ 1,579 a³ (a = latura)
Poliedru dual	trapezoedru pentagonal
Proprietăți	convexă, cu fețe poligoane regulate
Figura vârfului

Desfășurată

În geometrie antiprisma pentagonală este a treia dintr-o familie infinită de antiprisme, fiind formată dintr-un număr par de fețe triunghiulare dintre două fețe poligonale de capăt.

Antiprisma pentagonală regulată

Dacă toate fețele sale sunt poligoane regulate, este un poliedru semiregulat, cu indicele uniform U_77c. Poate fi considerat un icosaedru parabidiminuat, o formă obținută prin îndepărtarea a două piramide pentagonale dintr-un icosaedru regulat lăsând două fețe pentagonale neadiacente; o formă înrudită, icosaedrul metabidiminuat (unul dintre poliedrele Johnson), este și el format prin îndepărtarea a două piramide dintr-un icosaedru, dar fețele sale pentagonale sunt adiacente una cu cealaltă. Cele două fețe pentagonale ale oricărei forme pot fi augmentate cu piramide pentru a forma icosaedrul.

În cazul unei baze regulate cu 5 laturi, de obicei se consideră cazul în care copia sa este răsucită cu un unghi de $36°$ . O regularitate suplimentară se obține când dreapta care leagă centrele bazelor este perpendiculară pe planele bazelor, făcându-o antiprismă dreaptă. Ca fețe, are cele două baze pentagonale, conectate prin 10 triunghiuri isoscele. Având 12 fețe, este un dodecaedru neregulat.

Mărimi asociate

Pentru o antiprismă cu baza pentagonală regulată cu latura $a$ , înălțimea $h$ , aria $A$ și volumul se pot calcula cu relațiile formula:^[1]^[2]

h={\sqrt {\frac {5+{\sqrt {5}}}{10}}}\,a\approx 0,850651\,a\,,

A={\frac {{\sqrt {5(5+2{\sqrt {5}})}}+5{\sqrt {3}}}{2}}\,a^{2}\approx 7,771082\,a^{2},

V={\frac {5+2{\sqrt {5}}}{6}}\,a^{3}\approx 1,578689\,a^{3}.

Antiprismă autointersectată

O antiprismă pentagonală autointersectată este un poliedru stelat, identic din punct de vedere topologic cu antiprisma pentagonală convexă, cu același aranjament al vârfurilor, dar nu este un poliedru uniform deoarece laturile sunt triunghiuri isoscele. Configurația vârfului este 3.3/2.3.5, cu un triunghi retrograd. Are simetria D_5d de ordinul 20.

Politopuri înrudite

Antiprisma pentagonală apare ca element constitutiv în unele politopuri din dimensiuni superioare. Două inele a câte 10 antiprisme pentagonale delimitau fiecare suprafața marii antiprisme cvadridimensionale. Dacă aceste antiprisme sunt augmentate cu prisme și piramide pentagonale și legate cu inele formate din câte 5 tetraedre fiecare, se obține 600-celule.

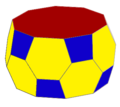
Antiprisma pentagonală poate fi trunchiată și alternată pentru a forma o antiprismă snub:

Antiprisme snub
Antiprismă A5	Trunchiată tA5	Alternată htA5

s{2,10}	ts{2,10}	ss{2,10}
v:10; e:20; f:12	v:40; e:60; f:22	v:20; e:50; f:32

Familia antiprismelor n-gonale uniforme v • d • m
Imagine poliedru												...	Antiprismă apeirogonală
Imagine pavare sferică												Imagine pavare plană
Configurația vârfului n.3.3.3	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3	...	∞.3.3.3