Rotondă pentagonală giroalungită
În acest articol, ne vom adânci în lumea fascinantă a lui Rotondă pentagonală giroalungită, un subiect care a stârnit interesul și curiozitatea a nenumărate persoane de-a lungul timpului. Rotondă pentagonală giroalungită este un element prezent în diverse fațete ale vieții de zi cu zi, de la istorie la știință, prin artă și cultură. În acest sens, vom explora diferitele aspecte care fac din Rotondă pentagonală giroalungită un subiect demn de a fi abordat și analizat în detaliu. De la origini și până la impactul său asupra societății de astăzi, ne vom cufunda într-o călătorie de descoperire și cunoaștere care ne va permite să înțelegem mai bine importanța și relevanța lui Rotondă pentagonală giroalungită în lumea din jurul nostru.
| Rotondă pentagonală giroalungită | |
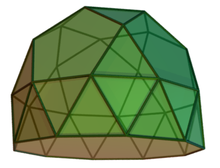 | |
| (model 3D) | |
| Descriere | |
|---|---|
| Tip | poliedru Johnson J24 – J25 – J26 |
| Fețe | 37 (30 triunghiuri echilaterale, 6 pentagoane regulate, 1 decagon regulat)[1] |
| Laturi (muchii) | 65[1] |
| Vârfuri | 30[1] |
| χ | 2 |
| Configurația vârfului | 2×5 (3.5.3.5); 2×5 (33.10); 10 (34.5) |
| Grup de simetrie | C5v, , (*55), ordin 10 |
| Arie | ≈ 31,007 a2 (a = latura) |
| Volum | ≈ 13,667 a3 (a = latura) |
| Poliedru dual | C1000dJ25[2] |
| Proprietăți | convexă |
| Desfășurată | |
 | |
În geometrie rotonda pentagonală giroalungită este un poliedru convex construit prin alungirea unei rotonde pentagonale (J6) prin atașarea unei antiprisme decagonale (în loc de o prismă decagonală, ca la poliedrul J21) la baza acesteia, ceea ce se reflectă în denumire prin prefixul „giro”. Este poliedrul Johnson J25. Având 37 de fețe, este un triacontaheptaedru.
Poliedre înrudite
Rotonda pentagonală giroalungită poate fi văzută și ca o birotondă pentagonală giroalungită (J48) cu o rotondă pentagonală îndepărtată. Ca la toate rotondele, poligonul bazei are de două ori mai multe laturi decât cel din partea de sus (în acest caz, poligonul de jos este un decagon, iar cel de sus este un pentagon).
Poliedru dual
Dualul rotondei pentagonale giroalungite are 30 de fețe: 10 romboizi, 10 patrulatere și 10 romburi:[2]
| Dualul rotondei pentagonale giroalungite | Desfășurata dualului |
|---|---|

|

|
Mărimi asociate
Următoarele formule pentru arie A și volum V sunt stabilite pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:[1]
Volumul se calculează pe baza rădăcinii polinomului[1]
din vecinătatea punctului , adică
Note
- ^ a b c d e en Stephen Wolfram, "Gyroelongated pentagonal rotunda" from Wolfram Alpha. Retrieved July 07, 2022.
- ^ a b en C1000dJ25, polyHedronisme v.0.2.1, accesat 2022-07-07



