Ortobicupolă triunghiulară
În acest articol vom explora subiectul Ortobicupolă triunghiulară și impactul său asupra societății de astăzi. De ani de zile, Ortobicupolă triunghiulară este obiect de studiu și interes datorită relevanței sale în diverse domenii, atât la nivel personal, cât și profesional. De-a lungul istoriei, Ortobicupolă triunghiulară a jucat un rol fundamental în evoluția umanității, influențând indivizi, comunități și culturi din întreaga lume. De la origini până la situația actuală, Ortobicupolă triunghiulară a generat dezbateri, cercetări și reflecții care au contribuit la extinderea înțelegerii noastre asupra acestui subiect. În acest sens, este esențial să analizăm critic importanța Ortobicupolă triunghiulară astăzi și modul în care prezența sa continuă să modeleze modul în care interacționăm și funcționăm în societatea actuală.
| Ortobicupolă triunghiulară | |
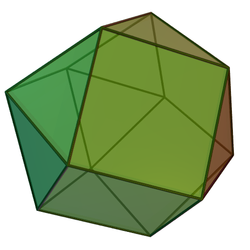 | |
| (model 3D) | |
| Descriere | |
|---|---|
| Tip | poliedru Johnson J26 – J27 – J28 |
| Fețe | 14 (8 triunghiuri echilaterale, 6 pătrate)[1] |
| Laturi (muchii) | 24[1] |
| Vârfuri | 12[1] |
| χ | 2 |
| Configurația vârfului | 6 (32.42), 6 (3.4.3.4) |
| Grup de simetrie | D3h, , (*223), ordin 12 |
| Arie | ≈ 9,464 a2 (a = latura) |
| Volum | ≈ 2,357 a3 (a = latura) |
| Poliedru dual | Dodecaedru trapezorombic |
| Proprietăți | convexă |
| Desfășurată | |
 | |
În geometrie ortobicupola triunghiulară sau anticuboctaedrul este un poliedru convex construit prin unirea a două cupole triunghiulare (J3) prin bazele lor mari. Este prima din șirul infinit de bicupole. Este poliedrul Johnson J27. Având 14 de fețe, este un tetradecaedru.
Are un număr egal de pătrate și triunghiuri echilaterale la fiecare vârf, însă nu este tranzitivă pe vârfuri. Având o sferă mediană, este un poliedru canonic.
Relația cu cuboctaedrele
| Ortobicupolă triunghiulară | Girobicupolă triunghiulară |
|---|---|

|

|
| Atât ortobicupola triunghiulară, cât și cuboctaedrul (girobicupola triunghiulară) conțin câte un hexagon central regulat. Ele pot fi divizate prin acest hexagon în perechi de cupole triunghiulare. | |
Ortobicupola triunghiulară are o oarecare asemănare cu cuboctaedrul, care ar fi similar cu girobicupola triunghiulară din nomenclatura poliedrelor Johnson — diferența este că cele două cupole triunghiulare care alcătuiesc ortobicupola triunghiulară sunt unite astfel încât perechi de fețe identice sunt adiacente (deci, „orto”); cuboctaedrul este îmbinat astfel încât triunghiurile sunt vecine cu pătratele și invers. Având în vedere o ortobicupolă triunghiulară, o rotație de 60° a unei cupole înainte de îmbinare dă un cuboctaedru. Prin urmare, un alt nume pentru ortobicupola triunghiulară este „anticuboctaedrul”.
Ortobicupola triunghiulară alungită (J35), care este construită prin alungirea ortobicupolei triunghiulare, are o relație specială (diferită) cu rombicuboctaedrul.
Dualul ortobicupolei triunghiulare este dodecaedrul trapezorombic, care are 6 fețe rombice și 6 trapezoidale și este similar cu dodecaedrul rombic.
Mărimi asociate
Următoarele formule pentru arie, A, volum, V, și raza sferei circumscrise, C sunt stabilite pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:[1]
Raza sferei circumscrise unei ortobicupole triunghiulare este același cu lungimea laturii (C = a).
Poliedre și faguri înrudiți
Fagurele cubic rectificat poate fi divizat și reconstruit ca o rețea de umplere a spațiului cu ortobicupole triunghiulare și piramide pătrate.[2]
Note
- ^ a b c d Stephen Wolfram, "Triangular orthobicupola" from Wolfram Alpha. Retrieved July 23, 2010.
- ^ en „J27 honeycomb”.

