Bipiramidă pentagonală

Descriere
Bipiramidă pentagonală

(model 3D)
Tip	poliedru Johnson (deltaedru) J₁₂ – J₁₃ – J₁₄
Fețe	10 (triunghiuri echilaterale)
Laturi (muchii)	15
Vârfuri	7
χ	2
Configurația vârfului	2 (3⁵); 5 (3⁴)
Configurația feței	V4.4.5
Simbol Schläfli	{ } + {5}
Diagramă Coxeter
Grup de simetrie	D_5h, , (*225), ordin 20
Arie	≈ 4,330 a² (a = latura)
Volum	≈ 0,603 a³ (a = latura)
Poliedru dual	prismă pentagonală
Proprietăți	convexă, tranzitiv pe fețe
Desfășurată

În geometrie bipiramida pentagonală este un poliedru convex construit prin lipirea a două piramide pentagonale la bazele lor pentagonale (care trebuie să fie congruente). Dacă fețele sunt regulate, este poliedrul Johnson (J₁₃ ) și poate fi văzut ca două poliedre Johnson J₂ lipite la baze. Având 10 fețe, este un decaedru. Este dualul prismei pentagonale (care este un poliedru uniform).

Deși are un singur tip de fețe, triunghiulare — deci este un deltaedru — chiar dacă fețele sunt regulate și congruente și este tranzitivă pe fețe, nu este un poliedru platonic deoarece în unele vârfuri se întâlnesc câte patru fețe, iar în altele câte cinci.

Bipiramida pentagonală este 4-conexă, ceea ce înseamnă că este nevoie de eliminarea a patru vârfuri pentru a deconecta vârfurile rămase. Este unul dintre cele patru poliedre simpliciale bine acoperite^⁠(d) cu patru conexiuni, ceea ce înseamnă că toate mulțimile independente maximale ale vârfurilor sale au aceeași mărime. Celelalte trei poliedre cu această proprietate sunt octaedrul regulat, bisfenoidul snub și un poliedru neregulat cu 12 vârfuri și 20 de fețe triunghiulare.^[1]

Mărimi asociate

Următoarele formule pentru înălțime $h$ , arie $A$ și volum sunt stabilite pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) $a$ :^[2]

h={\sqrt {2-{\frac {2}{\sqrt {5}}}}}\,a\approx 1,051462\,a\,,

A={\frac {5{\sqrt {3}}}{2}}a^{2}\approx 4,330127\,a^{2},

V={\frac {5+{\sqrt {5}}}{12}}a^{3}\approx 0,603006\,a^{3}.

Poliedru dual

Poliedrul dual al bipiramidei pentagonale este prisma pentagonală, cu șapte fețe: două pentagoane regulate paralele legate printr-un lanț de cinci dreptunghiuri. Deși prisma pentagonală are o formă care este un poliedru uniform (cu fețe pătrate), dualul formei Johnson a bipiramidei are mai degrabă fețe dreptunghiulare decât pătrate și nu este uniformă.

Dualul bipiramidei pentagonale	Desfășurata dualului

Poliedre înrudite

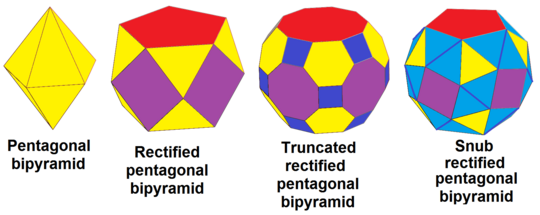
Bipiramida pentagonală, dt{2,5}, poate fi, succesiv, rectificată rdt{2,5}, trunchiată trdt{2,5} și alternată (snub) srdt{2,5}:

Bipiramide n-gonale (simetrice) drepte „regulate”:
Numele bipiramidei	Bipiramidă digonală	Bipiramidă triunghiulară (v. J₁₂)	Bipiramidă tetragonală (v. O)	Bipiramidă pentagonală (v. J₁₃)	Bipiramidă hexagonală	Bipiramidă heptagonală	Bipiramidă octogonală	Bipiramidă eneagonală	Bipiramidă decagonală	...	Bipiramidă apeirogonală
Imagine										...
Pavare sferică										Pavare plană
Config. feței	V2.4.4	V3.4.4	V4.4.4	V5.4.4	V6.4.4	V7.4.4	V8.4.4	V9.4.4	V10.4.4	...	V∞.4.4
Diagramă Coxeter										...

Note

^ en Finbow, Arthur S.; Hartnell, Bert L.; Nowakowski, Richard J.; Plummer, Michael D. (2010), „On well-covered triangulations. III”, Discrete Applied Mathematics, 158 (8): 894–912, doi:10.1016/j.dam.2009.08.002 , MR 2602814
^ es Sapiña, R. „Area and volume of the Johnson solid J₁₃”. Problemas y ecuaciones. ISSN 2659-9899. Accesat în 4 septembrie 2020.

Legături externe

Portal Matematică

Materiale media legate de bipiramidă pentagonală la Wikimedia Commons
en Eric W. Weisstein, Pentagonal dipyramid la MathWorld.
en Eric W. Weisstein, Dipyramid la MathWorld.
en Conway Notation for Polyhedra Cheie: dP5

[1] Finbow, Arthur S.; Hartnell, Bert L.; Nowakowski, Richard J.; Plummer, Michael D. (2010), „On well-covered triangulations. III”, Discrete Applied Mathematics, 158 (8): 894–912, doi:10.1016/j.dam.2009.08.002 , MR 2602814

[pye-2] s Sapiña, R. „Area and volume of the Johnson solid J₁₃”. Problemas y ecuaciones. ISSN 2659-9899. Accesat în 4 septembrie 2020.

[1]

[2]